Towards real-time numerical simulations of human-environment systems: data assimilation & agent-based modelling
Applications to real pedestrian traces and gate selection problems with Particle Filters
Patricia Ternes and Nick Malleson
Slides available at:
https://urban-analytics.github.io/dust/presentations.html
https://patricia-ternes.github.io/presentations.html



StationSim
Agent-based model

- Try to follow an ideal path (linear) towards the exit point.
- If the ideal path is blocked, try to perform a deviation
- If both the ideal path and the deviation positions are blocked, stay still until one of them becomes vacant.

Dependence level
Local geographic density
$$ \rho_{i,t} = n_{i,t} \frac{r^{2}}{(R^{2} - r^{2})} $$
- \(n_{i,t}\): number of neighbours agents
- \(r=0.5\) m
- \(R=5\) m
- \(0\le \rho \le 1\)
Agent direction of movement
$$ \theta_{i,t} \sim \mathcal{N}(0, [180^{\circ}\rho_{i,j}]^2) $$
- \(\theta_{i,t}\): deviation angle
Agent speed
$$ v_{i,t} = v_{i,max}(1 - \rho_{i,t}) $$
- \(v_{i,max}\): maximum speed

Agent direction of movement
$$ \theta_{i,t} \sim \mathcal{N}(0, [180^{\circ}\rho_{i,j}]^2) $$
- \(\theta_{i,t}\): deviation angle
Agent speed
$$ v_{i,t} = v_{i,max}(1 - \rho_{i,t}) $$
- \(v_{i,max}\): maximum speed
Categorical Parameter
Continuous Parameter
Pedestrians Trajectories & Model Prediction
274 agents + Initial conditions + speed + exit gate
- Solid lines: pedestrians
- Dashed lines: agents
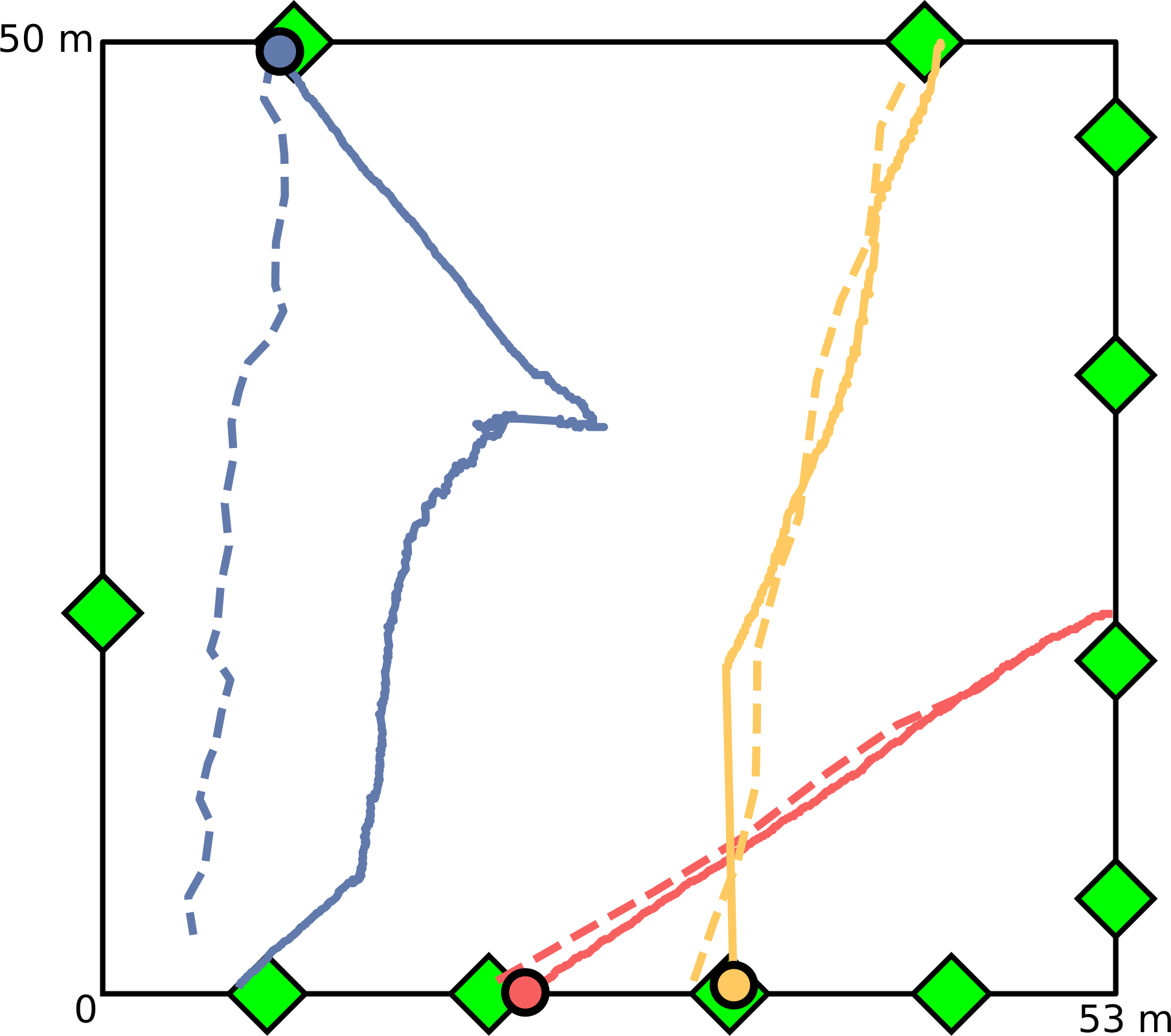
- Correct: RSME \(\le\) 4.25 m
- Good: 4.25 m \(<\) RSME \(\le\) 8.50 m
- Poor: RSME > 8.50 m

Model Prediction & Unknown Parameters
274 agents + Initial conditions + speed + exit gate
- Speed from \(\mathcal{N}(1.6\hbox{~m/s},(0.6\hbox{~m/s})^2)\)
- Exit Gate from \(P(g_{out}~|~g_{in}) = \left\{ \begin{array}{ccl} 0 & \text{if} & g_{out} \text{ and } g_{in} \text{ are on the same side}, \\ \frac{1}{G-G_{in}} & \text{if} & g_{out}\text{ and } g_{in} \text{ are on different sides} \end{array}\right.\)


Particle Filter
Sequential Importance Resampling
- One agent per simulation, 100 particles, data assimilation window of 25 frames.
- \(\rho_{i,t}\) randomly drawn from an exponential distribution with rate parameter of 25.3
- 274 pedestrians
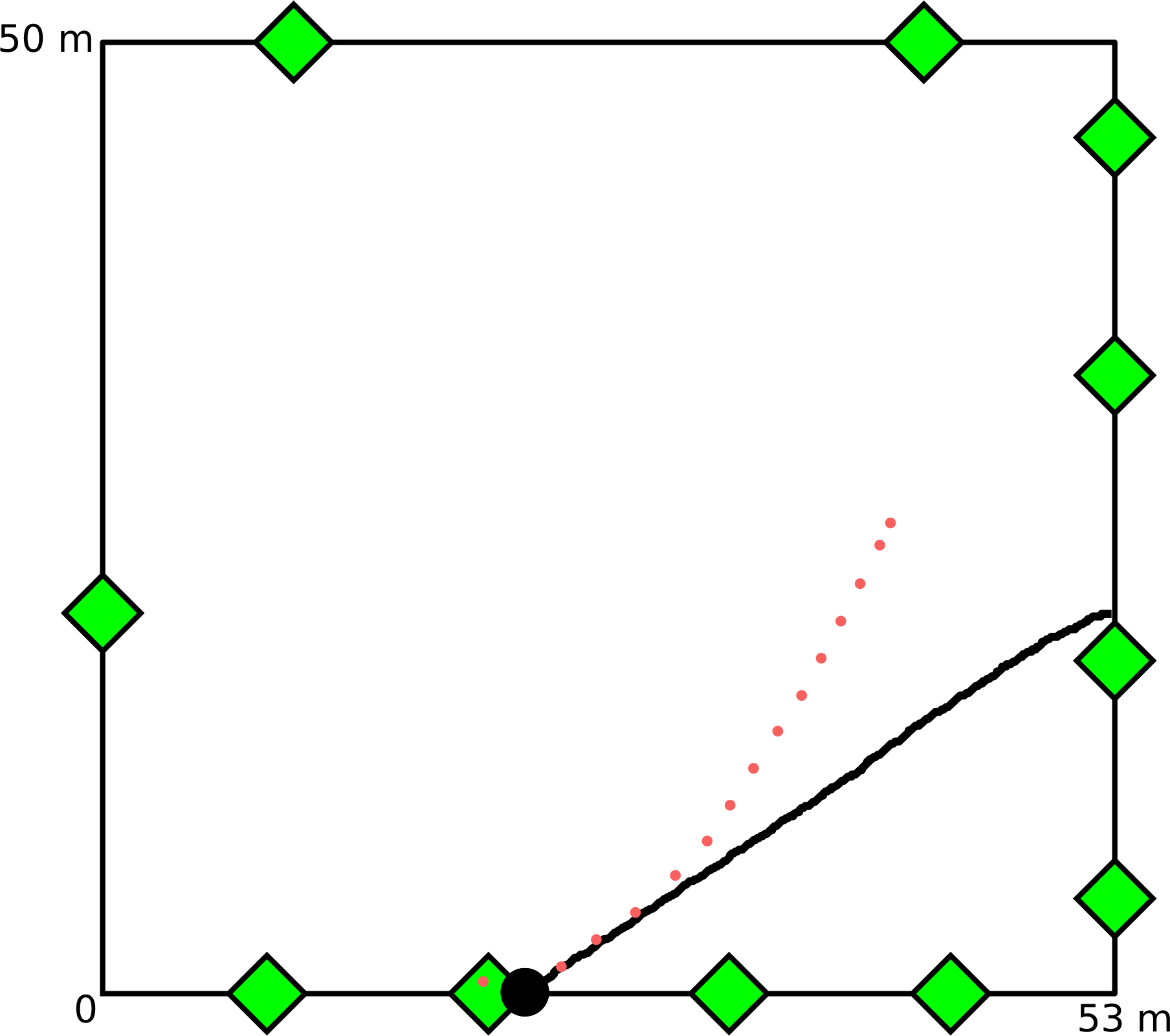

Categorical-Continuous Particle Filter
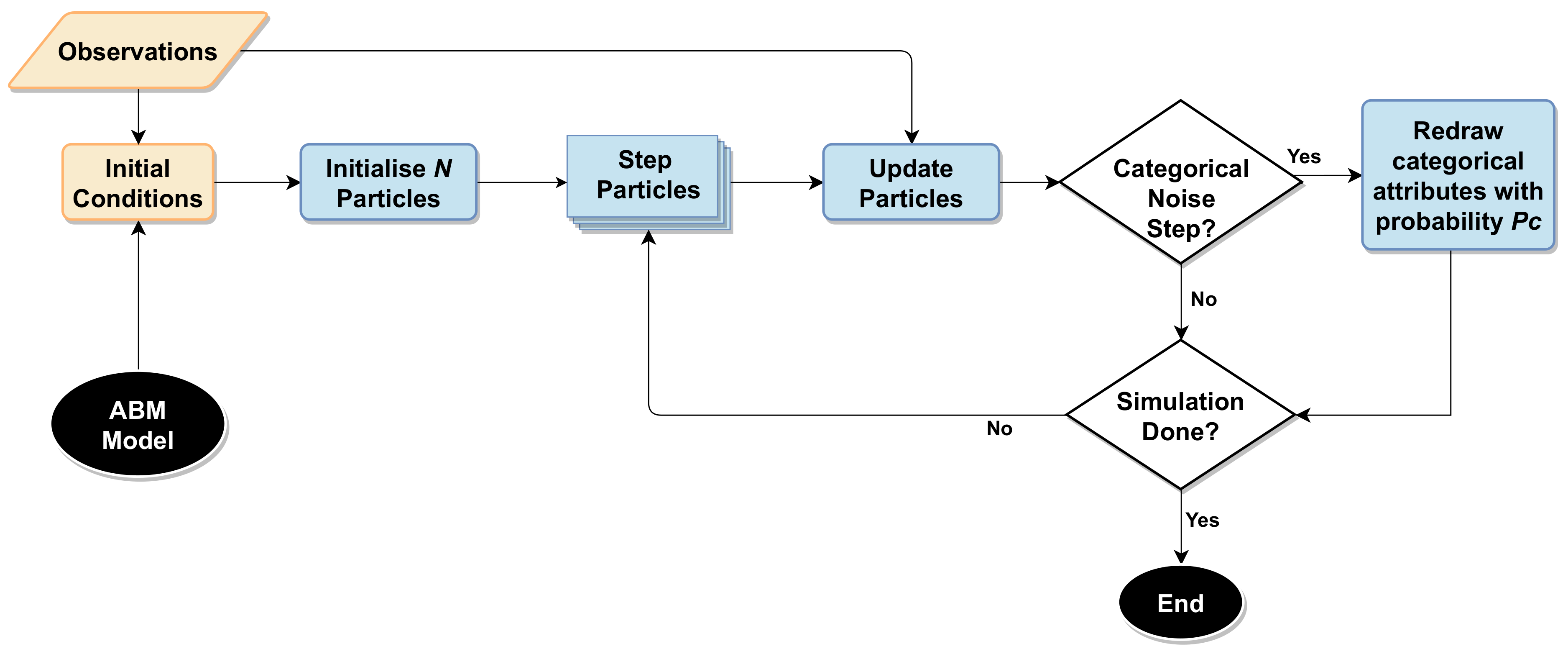
Categorical Noise Step
try to perturb the categorical unknown parameters
- the agent \(i\) has a probability \( P_c \) of having its categorical parameter \(j\) redefined
- Redrawn probability: \( P_c \)
- the categorical parameter \(j\) is redefined according a transition matrix \(T_j\)
- each categorical parameter has a specific transition matrix
- the categorical noise step must be applied to all \(n\times N\) agents after the update step every \(W_c = \tau\times W_d\) time steps.
- Redrawn window: \(W_c\)
- Data assimilation window: \(W_d\)
Transition Matrix
StationSim + Grand Central Terminal
$$p(\text{ID}'~|~\text{ID}) = \left\{ \begin{array}{ccl} 0.4 & \text{for} & \text{ID}' = \text{ID}, \\ 0.25 & \text{for} & \text{ID}' = \text{ID} \pm 1, \\ 0.05 & \text{for} & \text{ID}' = \text{ID} \pm 2, \\ \end{array}\right.$$

Categorical-Continuous Particle Filter
- One agent per simulation, 100 particles, DA window of 25 frames, Redrawn window of 100 frames.
- \(\rho_{i,t}\) randomly drawn from an exponential distribution with rate parameter of 25.3
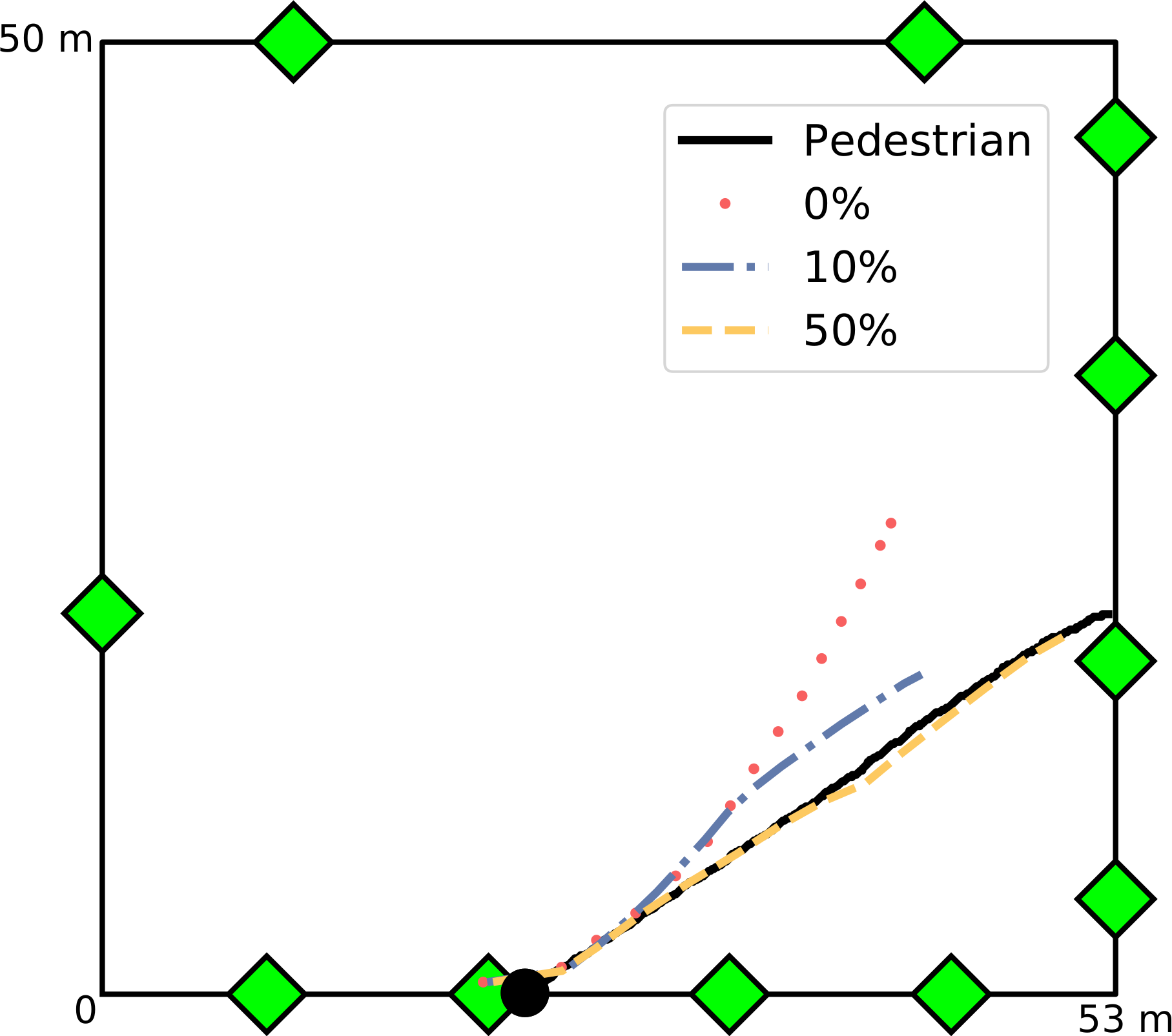
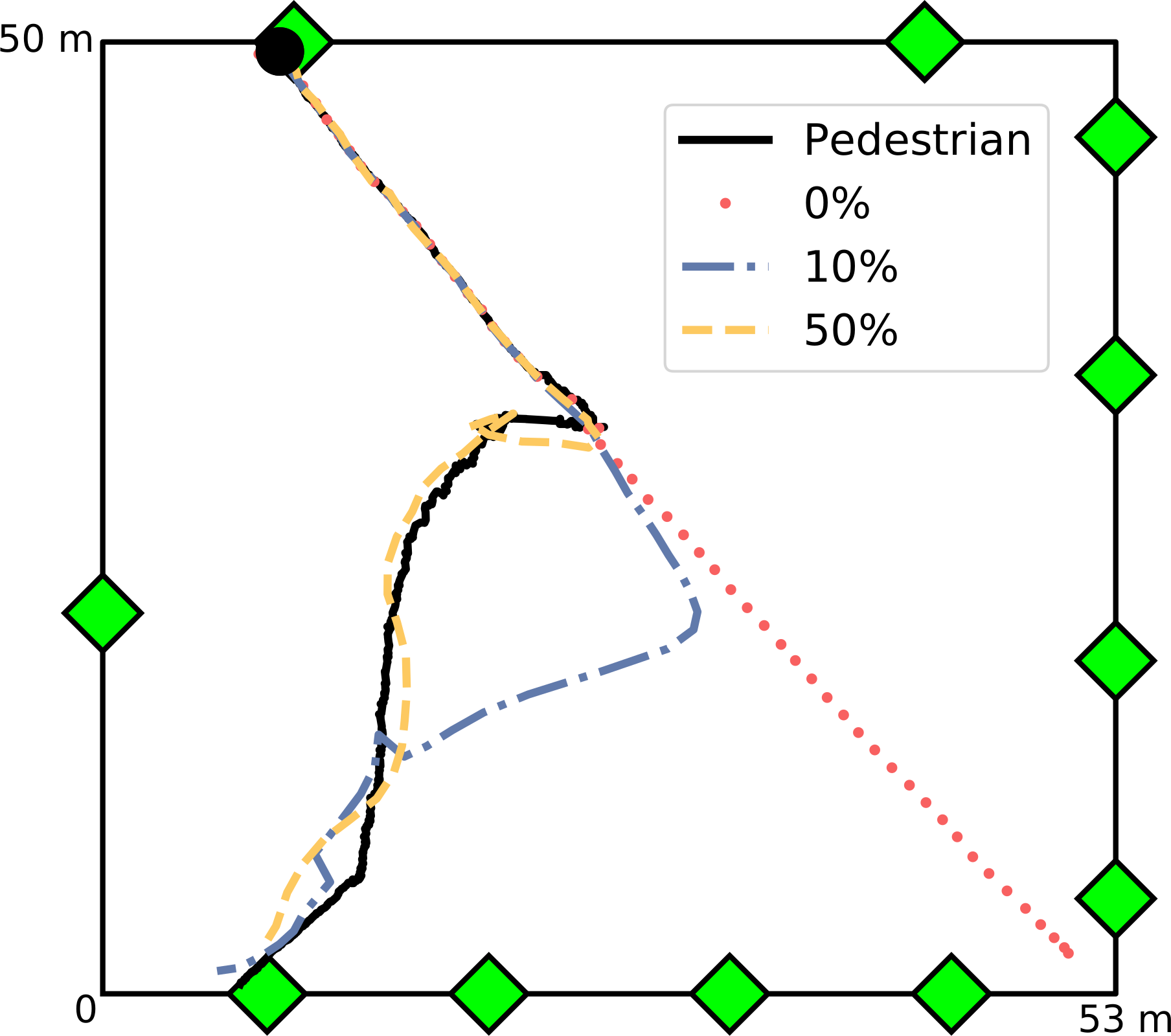
Categorical-Continuous Particle Filter
- One agent per simulation, 100 particles, DA window of 25 frames
- \(\rho_{i,t}\) randomly drawn from an exponential distribution with rate parameter of 25.3
- 274 pedestrians, 5 runs, 11 redrawn probabilities, 5 redrawn windows;

CCPF \(\times \) SIR-PF \(\times \) Model prediction
- Data Assimilation - One agent per simulation
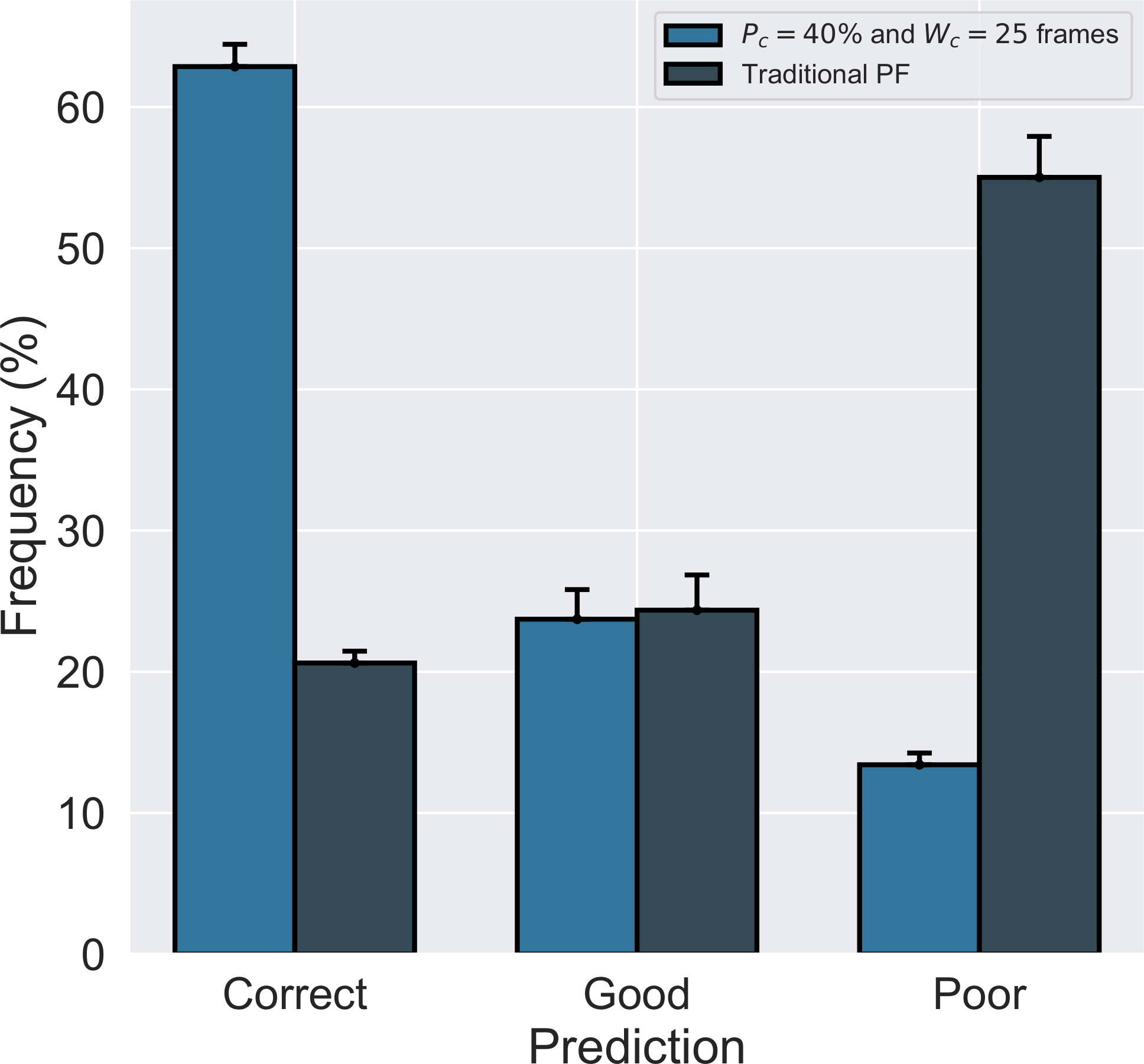
- Model prediction (unrealistic scenario)

Towards real-time numerical simulations of human-environment systems: data assimilation & agent-based modelling
Applications to real pedestrian traces and gate selection problems with Particle Filters
Patricia Ternes and Nick Malleson
Slides available at:
https://urban-analytics.github.io/dust/presentations.html
https://patricia-ternes.github.io/presentations.html


